DFS, BFS 는 graph 자료구조에서 탐색 알고리즘으로 깊이 우선 탐색(Depth First Search) , 너비 우선 탐색(Breadth First Search)의 약자입니다.

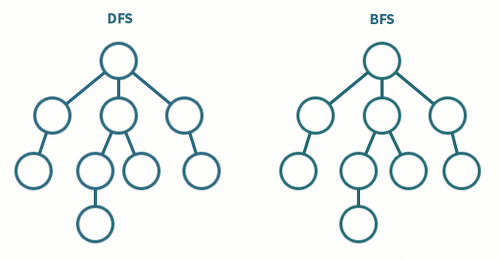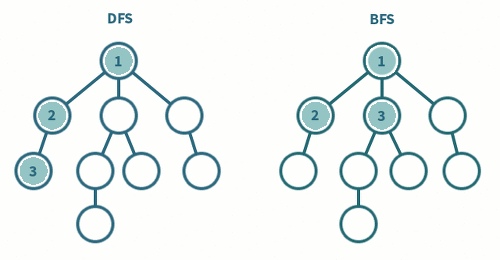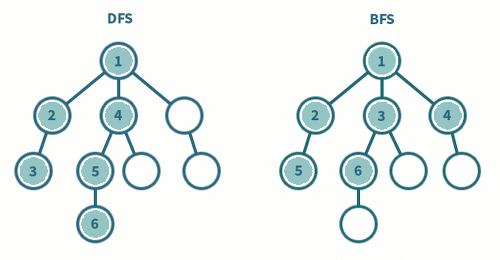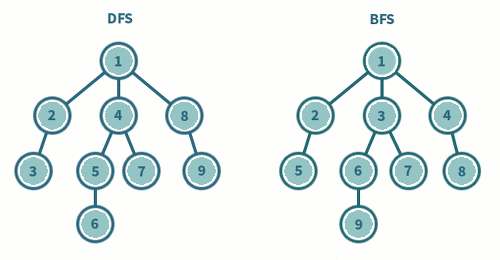
DFS, BFS 의 차이를 확실히 구별할 수 있습니다.
DFS 는 Leaf Node가 나올때까지 깊어져 가며 탐색하는 방법이고, BFS 는 갈림길이 모두 연결되어있는 Node 를 탐색해 나가는 방법입니다.

graph

그래프의 수학적 정의 입니다.

G = (V, E)

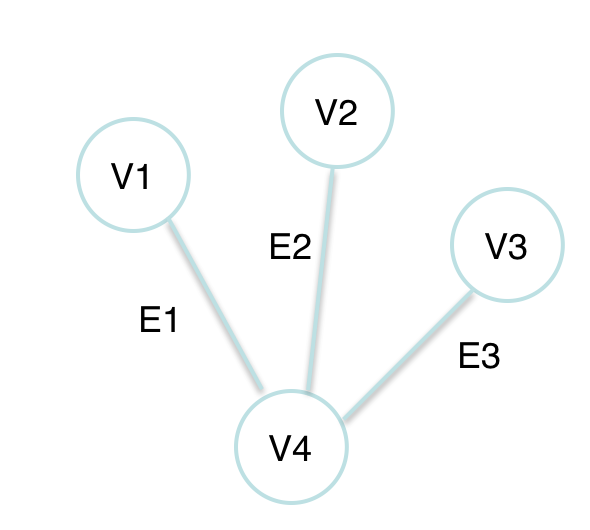
V 는 정점(vertex)으로 V1, V2, V3, V4가 해당합니다. E 는 간선(edge)로 정점들을 연결하는 부분집합을 말합니다. {(V,V4), (V2,V4), (v3,V4)} 가 해당합니다.

• 무방향 그래프 : 향성이 없는 그래프
  • (V1, V2) , (V2,V1) 이 동일합니다.
• 방향그래프 : 간선에 방향이 있는 그래프입니다.
  • (V1, V2)와 (V2, V1) 이 다른 간선입니다.

그래프를 구현하는 방법은 2가지가 있습니다. 인접행렬 과 인접리스트입니다.

인접행렬은 2차원 배열을 이용해서 그래프를 표현하는 방법입니다.

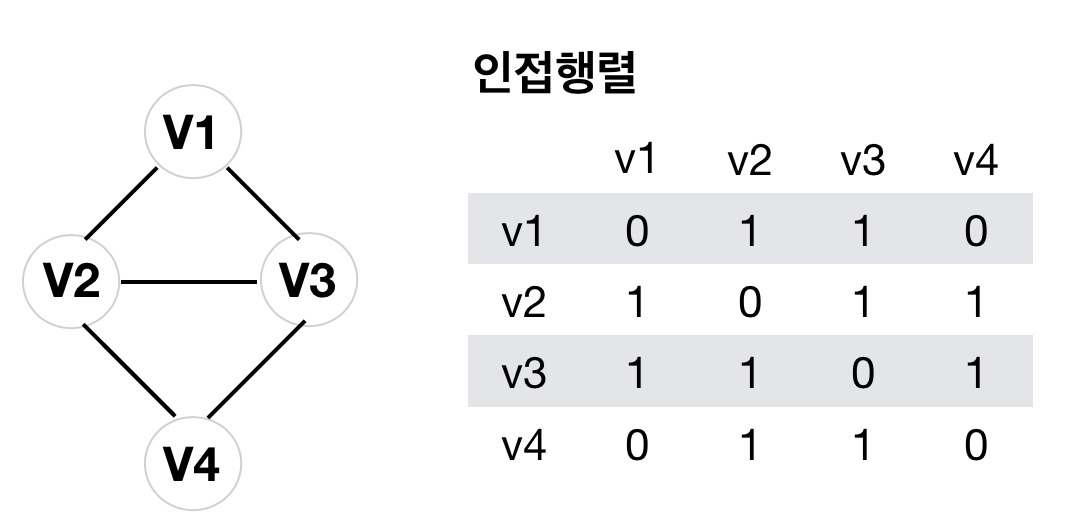
인접행렬은 vertex 의 n^2 의 공간이 필요합니다. 따라서 vertex가 적은 graph 일때 사용하면 효율적입니다.

인접리스트는 linked list를 사용합니다. vertex 개수에 따라 linked list 가 생성하며 vertex와 연결된 edge를 저장합니다. 각각의 연결리스트는 배열로 표현합니다.

graph 탐색

DFS 는 재귀호출, BFS는 queue 를 이용하여 구현할수 있습니다.

DFS

 final static boolean[][] ADJACENCY = {
            {false, false, false, false, true},
            {false, false, true, true, false },
            {false, true, false, true, true},
            {false, true ,true , false, true},
            {true, false, true, true, false},
    };

    static boolean[] VISITED = new boolean[ADJACENCY.length];


    public static void dfs(int value){


        VISITED[value] = true;
        System.out.println("value : " + value);
        for(int i = 0; i < ADJACENCY.length; i++ ){

            if(ADJACENCY[value][i] && !VISITED[i]){
                dfs(i);

            }
        }

    }

    public static void main(String[] args){

        dfs(0);

    }

BFS

 final static boolean[][] ADJACENCY = {
            {false, false, false, false, true},
            {false, false, true, true, false },
            {false, true, false, true, true},
            {false, true ,true , false, true},
            {true, false, true, true, false},
    };

    static boolean[] VISITED = new boolean[ADJACENCY.length];


    static Queue<Integer> q = new LinkedList<Integer>();

    public static void bfs(int value){

        q.add(value);
        VISITED[value] = true;

        while(!q.isEmpty()){

            int poll = q.poll();
            System.out.println("poll : " + poll);

            for(int i = 0 ; i < ADJACENCY.length; i ++){
                if(ADJACENCY[poll][i] && !VISITED[i]){
                    q.add(i);
                    VISITED[i] = true;
                }
            }

        }

    }

    public static void main(String[] args){
        bfs(0);
    }

graph cycle 판단

final static boolean[][] ADJACENCY = {
            {false, false, false, false, true},
            {false, false, true, true, false },
            {false, true, false, true, true},
            {false, true ,true , false, true},
            {true, false, true, true, false},
    };

    static boolean[] VISITED = new boolean[ADJACENCY.length];
    static Stack<Integer> s = new Stack<Integer>();

    public static boolean isCycle(int value){

        boolean isCycle = false;
        s.add(value);

        while(!s.isEmpty()){

            int current = s.pop();
            for(int i = 0 ; i< ADJACENCY[current].length; i++){
                if(ADJACENCY[current][i] && !VISITED[i]){
                    s.push(i);
                }
            }
            //cycle.add(current);
            if(VISITED[current]){
                isCycle = true;
            }else{
                VISITED[current] = true;
            }

        }

        return isCycle;

    }

    public static void main(String[] args){
        System.out.println(isCycle(0));
    }

---

출처

• [https://namu.wiki/w/BFS] (https://namu.wiki/w/BFS)