데이터베이스와 파일시스템에서 B-Tree를 많이 사용합니다.
rdb 인덱스 관련해서 정리해보다가 일반적으로 B-Tree , B+-Tree 자료구조를 사용하는것을 알게되었습니다.
B-Tree 자료 구조에 대해서 알아보도록 하겠습니다.
B-Tree
이진 트리가 자식 노드가 최대 2개인 노드를 말하는 것이라면 B-Tree는 자식 노드의 개수가 2개 이상인 트리를 말합니다.
또한 노드내의 데이터가 1개 이상일수가 있습니다. 노드내 최대 데이터 수가 2개라면 2차 B-Tree, 3개라면 3차 B-Tree 라고 말합니다.
‘1, 2, 3, … M차 B-Tree 라고 합니다.
차수가 홀수인지 짝수인지에 따라 알고리즘이 많이 달라집니다.
B-Tree 성립 조건에대해서 자세히 알아보겠습니다.
- 노드의 데이터수가 n개라면 자식 노드의 개수는 n+1 개입니다.
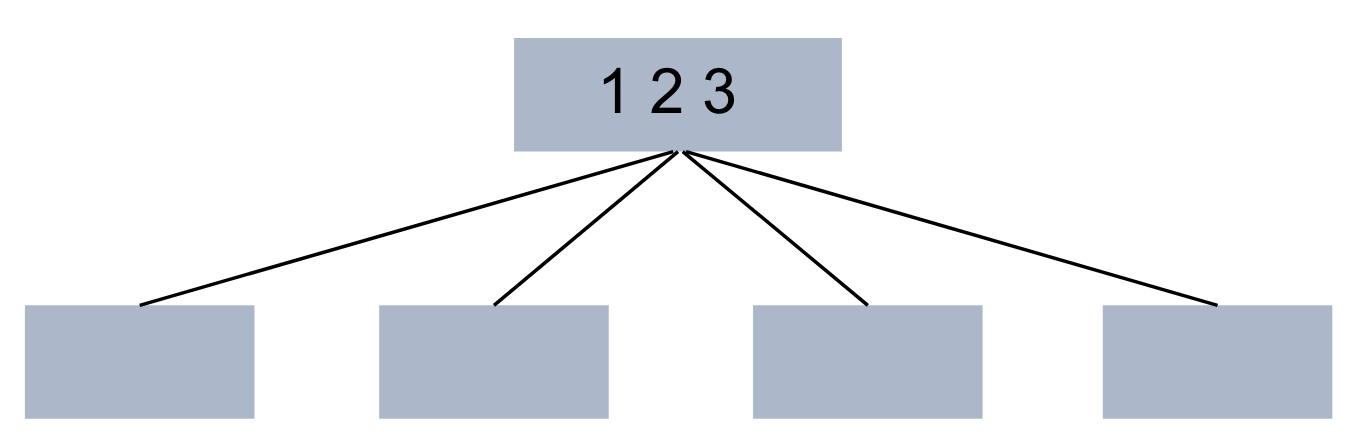
root노드에 데이터가 1, 2, 3 3개이므로 자식 노드의 개수는 4개 입니다. - 노드의 데이터는 반드시 정렬된 상태여야 합니다.
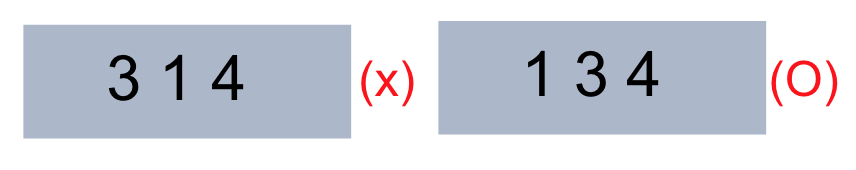
- 노드의 자식노드의 데이터들은 노드 데이터를 기준으로 데이터보다 작은 값은 왼쪽 서브 트리에 큰값들은 오른쪽 서브 트리에 이루어 져야 합니다.
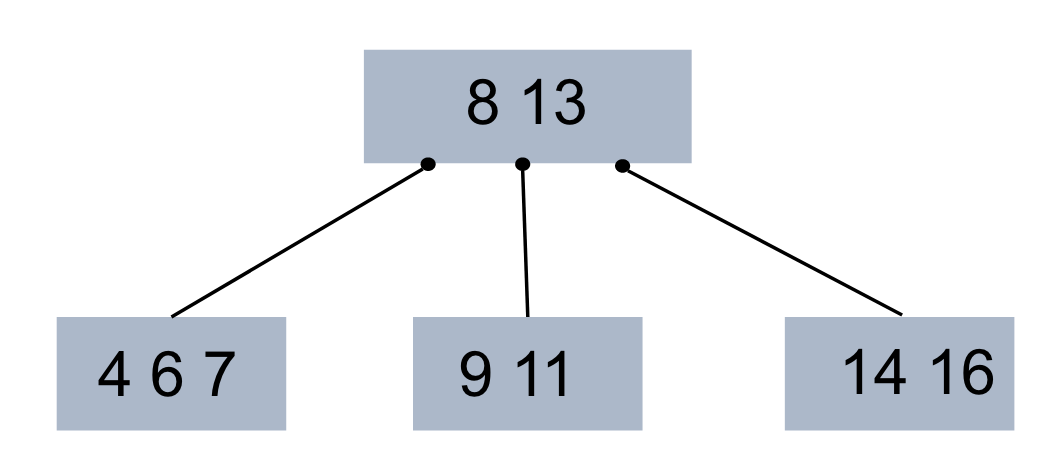
root노드의 데이터는 8, 13입니다.- 8보다 작은 데이터는 8의 왼쪽 서브트리에, 8과 13 사이의 값은 8의 오른쪽 13의 왼쪽 서브트리 (중간)에 , 13보다 큰값은 13 오른쪽 서브 트리에 값을 이루고 있습니다.
Root노드가 자식이 있다면 2개이상의 자식을 가져야 합니다.Root노드를 제외한 모든 노드는 적어도 M/2 개의 데이터를 갖고 있어야 합니다. 3차 B-Tree 까지는 1개의 데이터를 갖고 있어야 하니 고려하지 않아도 되는 조건인것 같습니다. 4차 부터는Root노드를 제외하고 노드가 최소 2개의 데이터를 갖고 있어야 합니다.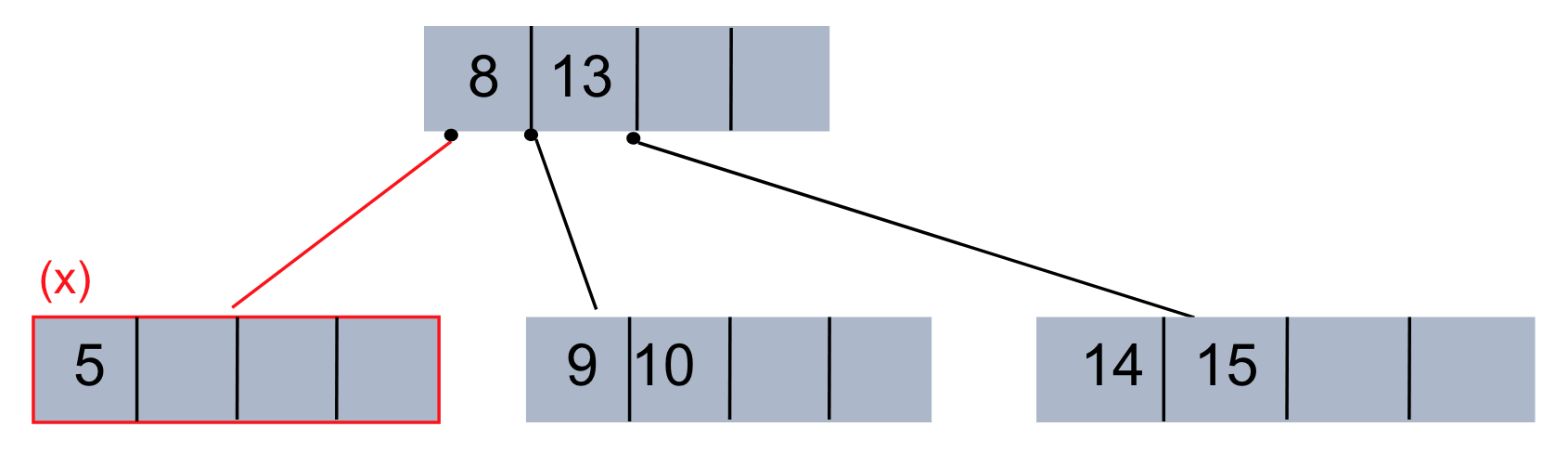
- 다음과 같은 4차 B-Tree 에서
Root노드의 데이터 8의 왼쪽 서브트리 노드가 데이터가 1개이므로 조건에 부합하지 않습니다.
- 다음과 같은 4차 B-Tree 에서
Leaf노드로 가는 경로의 길이는 모두 같아야 합니다. 즉Leaf노드는 모두 같은 레벨에 존재해야 합니다. 있어야 합니다.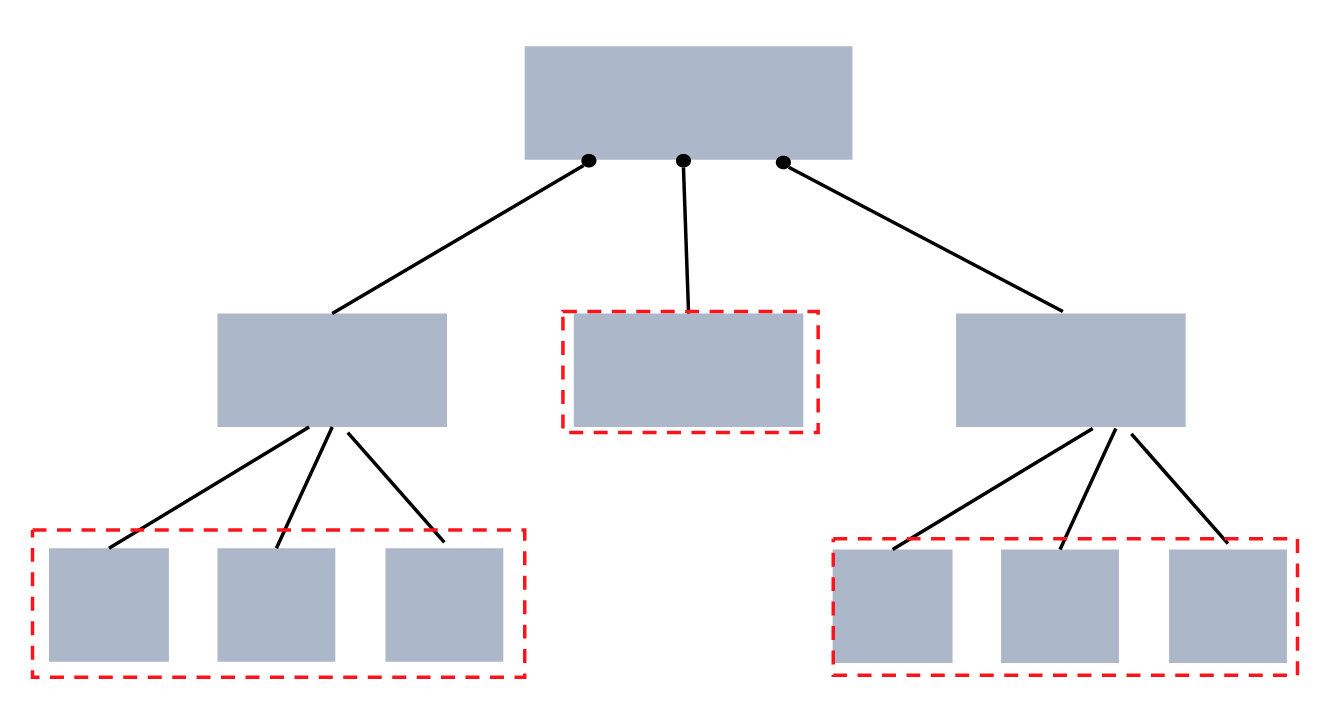
- 입력 자료는 중복될수 없습니다.
탐색
B-Tree 는 이진트리와 마찬가지로 작은 값은 왼쪽 서브트리, 큰 값은 오른쪽 서브트리에 이루어져있습니다.
탐색 하고자하는 값을 root 노드 부터 시작해 하향식으로 탐색해 나갑니다.
삽입
차수에 따라 B-Tree 알고리즘이 다릅니다.
저는 3차(홀수) B-Tree 를 예시로 들어보겠습니다.
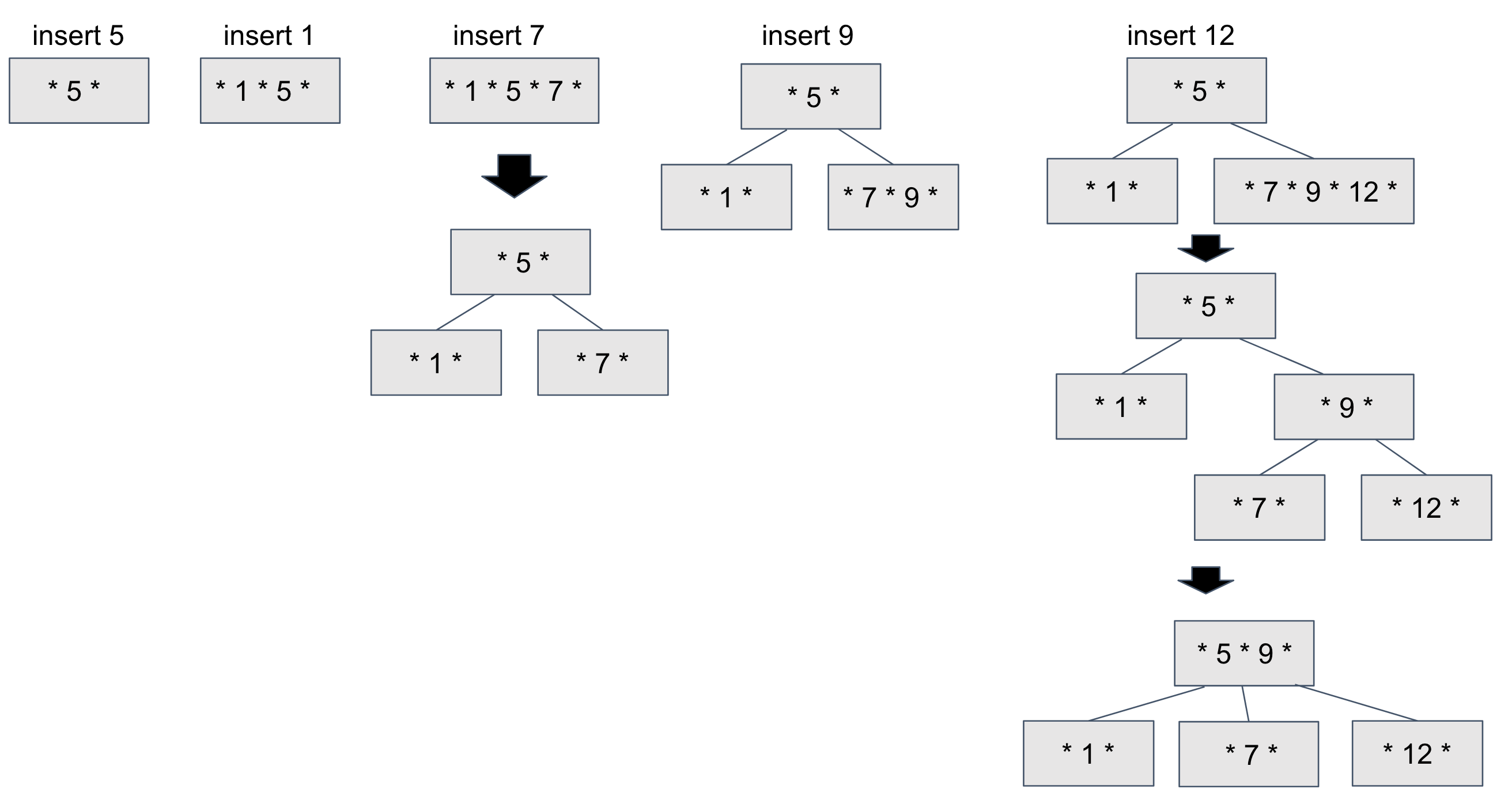
- 초기 삽입시에는
root노드를 생성합니다.
- 데이터를 탐색해 해당하는
Leaf노드에 데이터를 삽입합니다. Leaf노드 데이터가 가득 차 있으면 노드를 분리합니다.if(노드 데이터 개수 = M(차수))- insert7 에서 노드가 1, 5, 7 로 가득찼습니다.
- 정렬된 노드를 기준으로 중간값을 부모 노드로 해서 트리를 구성합니다.
- 분리한 서브트리가 B-Tree조건에 맞지 않는다면 부모 노드로 올라가며 merge합니다.
- insert12 에서
[9, 7, 12]를 서브트리로 분리 하였으나 B-Tree 조건에 맞지 않습니다.
Leaf노드가 모두 같은 레벨에 존재 하지 않습니다.
Root노드와 merge로 조건을 만족시켰습니다.
- insert12 에서
삭제
삭제는 크게 Leaf노드인 경우와 Leaf노드가 아닌경우로 나누어집니다.
몇가지 예로 알아보겠습니다.
예시1
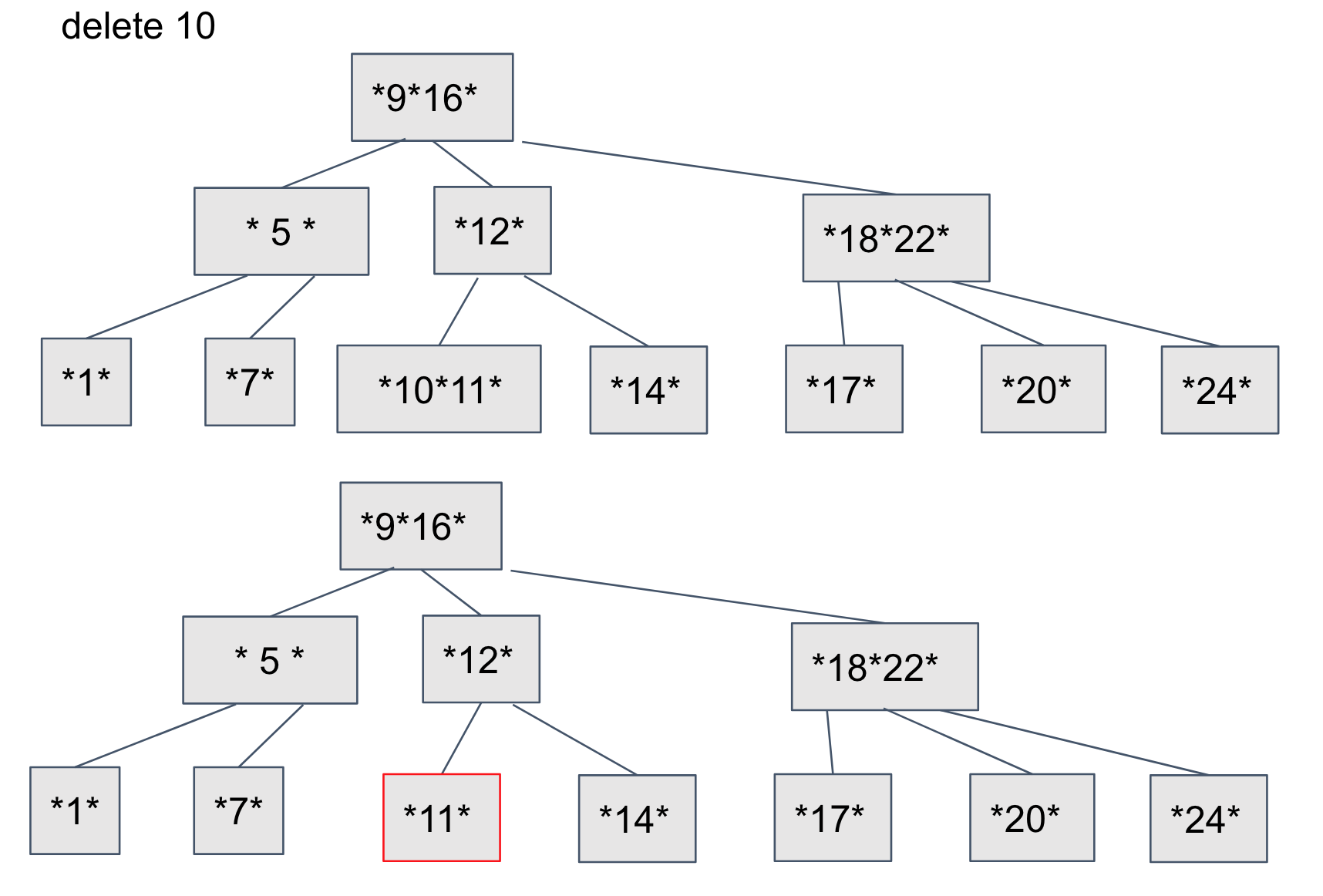Tree에서 10을 검색하고 Leaf노드이며, 노드에서 데이터를 삭제하여도 B-Tree를 유지 하고 있습니다.
예시2
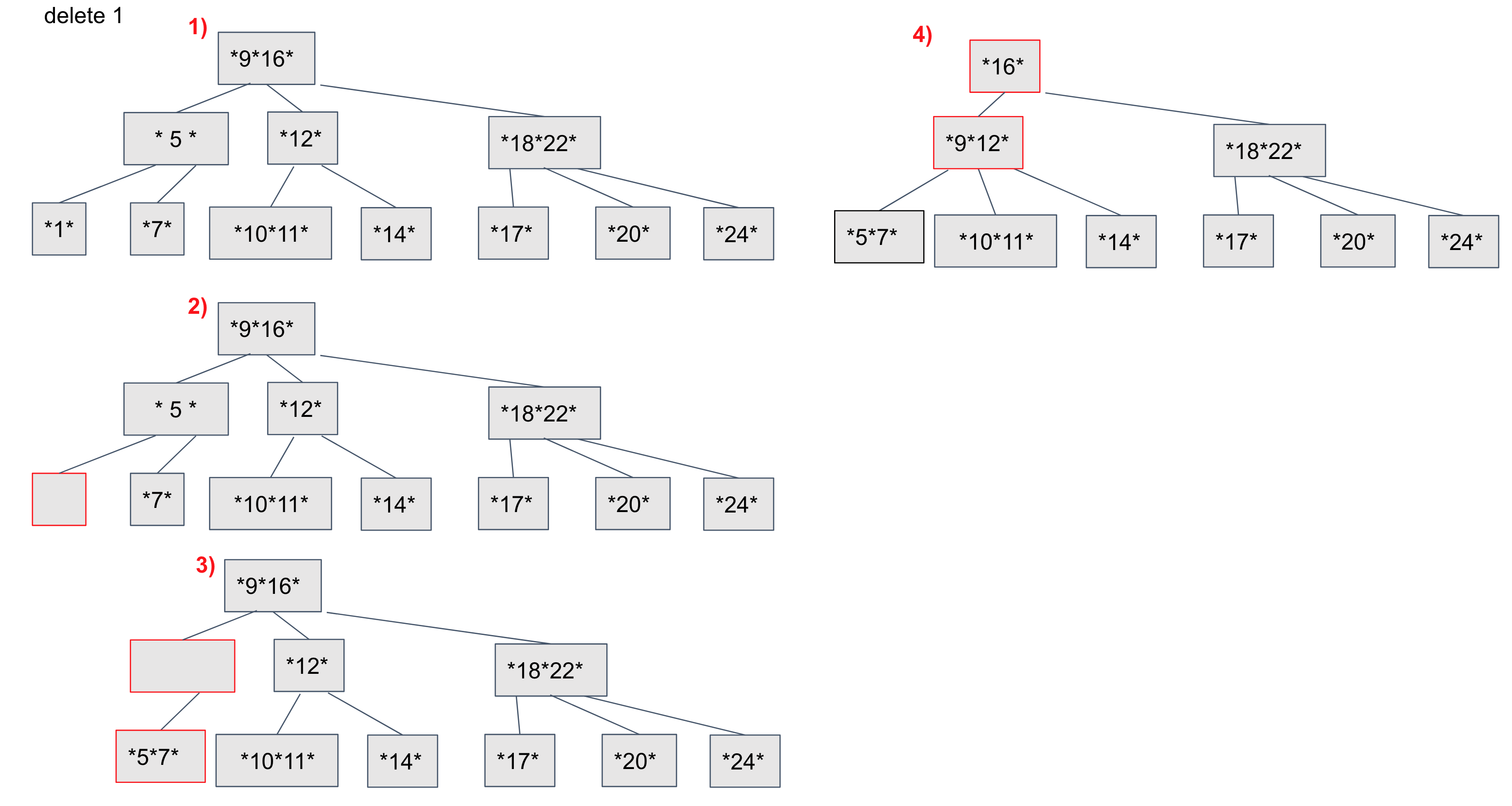
Leaf노드에서 1을 삭제하면 B-Tree 구조가 깨집니다.
삭제한 노드의 부모노드로 올라가며 데이터를 가져옵니다.
1의 부무노드와, 형제노드를 merge 합니다. 부모 노드에서 자식노드로 값을 가져오고 자식노드의 형제노드와 merge 합니다. root 노드 까지 올라가며 B-Tree 조건에 맞을때까지 이 작업을 반복합니다.
예시3
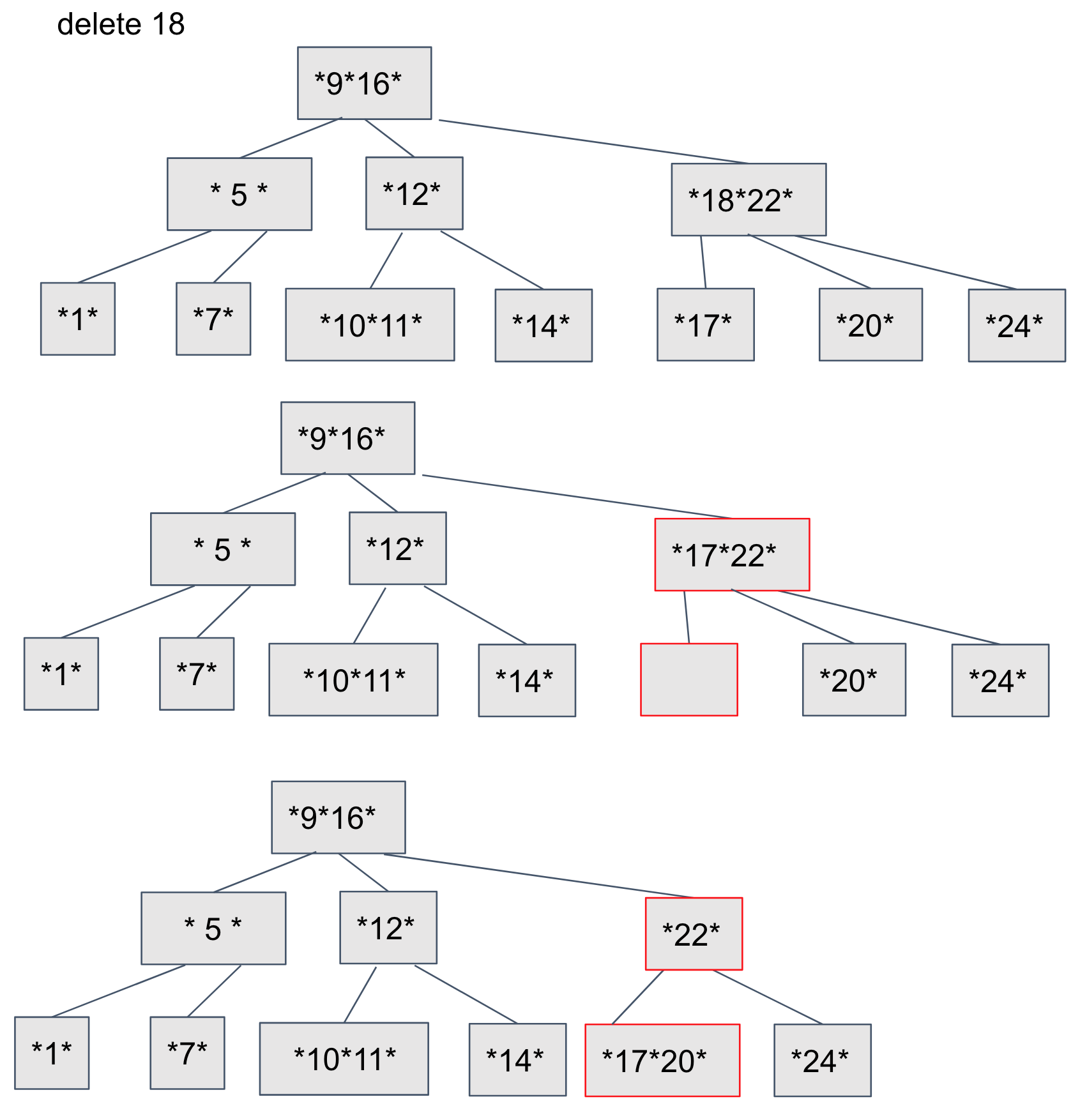
Leaf노드에 위치하지 않는 데이터를 삭제할 경우 입니다.
먼저, 노드에서 데이터를 삭제하고 왼쪽 서브트리에서 최대값을 노드에 위치시킵니다. 같은 방식으로 부모노드에서 자식노드로 값을 가져오고 형제노드와 merge 하며 B-Tree조건이 맞을때까지 반복합니다.
예시4
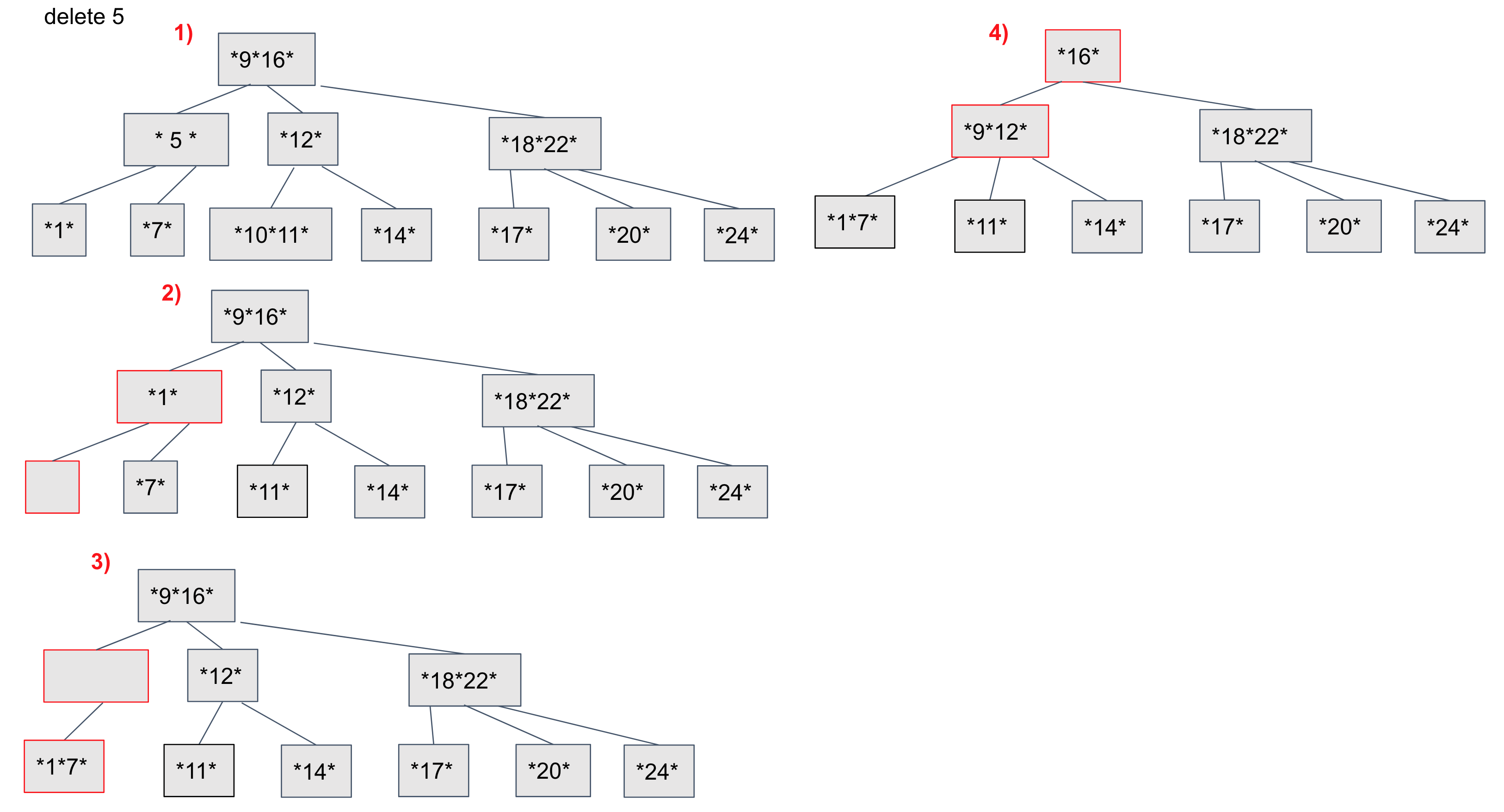
정리
B+-Tree와 같이 정리하려 했으나, 내용이 너무 길어질것 같아 같이 포스팅하지 못했습니다. 다음 포스팅에서 정리하도록 하겠습니다.